(Important note: To get the most out of the below case study, the solution report, which includes LP formulations, optimal values of the decision variables, and interpretations of the results, can be used as a companion.)
Case Definition
Can Caravan is a renowned caravan manufacturer, who offers a variety of 42 models to its customers. These 42 models are grouped under two main categories with respect to their manufacturing requirements, i.e. basic and pro series. For the June 2022-May 2023 period, the company wishes to develop an aggregate production plan.
The monthly demand forecast for different caravan series for the planning period is given below.
| Basic | Pro | |
|---|---|---|
| Jun.22 | 28 | 14 |
| Jul.22 | 20 | 10 |
| Aug.22 | 26 | 4 |
| Sep.22 | 24 | 4 |
| Oct.22 | 18 | 6 |
| Nov.22 | 10 | 8 |
| Dec.22 | 22 | 10 |
| Jan.23 | 20 | 12 |
| Feb.23 | 18 | 6 |
| Mar.23 | 32 | 8 |
| Apr.23 | 34 | 14 |
| May.23 | 36 | 6 |
Cost of producing a basic series caravan is estimated to be $6250, excluding cost of direct labour. This figure is $9750 for pro series caravans. Considering the direct labour requirements, a basic series product demands 380 man.hours for production, whereas a pro series caravan requires 530 man.hours. Holding cost of a basic caravan is estimated to be $250 per caravan per month, whereas it costs $500 to hold one unit of pro caravan in stock for a month. At the end of May 2022, the company projects to have 8 units of basic model, and 3 units of pro model caravans in it stocks.
Currently the company employs 86 assembly workers, who work 180 hours per month on average. Average monthly salary of an assembly worker is $420. Workers can be asked to work overtime, which is limited by 40 hours per month. The hourly fee for overtime is 50% more than the regular hourly fee.
Considering the administrative costs and inefficiencies during the orientation period, cost of employing a new worker is estimated to be $800 per worker. During lay-offs, the company pays $1400 per worker.
Base Problem
Formulate and solve the aggregate production planning problem. To develop the aggregate plan, you will need to construct and solve a linear programming problem minimizing the overall cost comprised of production, holding inventory and workforce related (regular time and overtime) costs. Shortages are not allowed. Draw a bar chart of monthly production and inventory for the board meeting. Comment on your plan including the total production, inventory, workforce used, and related costs.
In your solution to the base problem, investigate the inventory projections for both models. When is it optimal to carry base version in the inventory, and when is it optimal to carry the pro version in the inventory? When do you keep both models in the inventory? Explain.
Solution (Base Problem)
1
2
3
4
5
6
# Import libraries
from pulp import * # Will be used as the solver
import numpy as np
import matplotlib.pyplot as plt # Will be used to generate plots
1
2
3
4
5
# Definition of the problem
model = LpProblem( name = "aggregate-planning",
sense = LpMinimize )
1
2
3
4
5
6
# Definition of the sets
T = range(1,13) # Set of months: T = {1, 2, 3, 4 ... 12}
T_ext = range(13) # Extended time horizon T = 0 included
M = ("b", "p") # Set of aggregated product groups: basic and pro
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
# Definition of the parameters
D = ( (28, 14),
(20, 10),
(26, 4),
(24, 4),
(18, 6),
(10, 8),
(22, 10),
(20, 12),
(18, 6),
(32, 8),
(34, 14),
(36, 6) ) # Monthly demands
wInit = 86 # Initial # of workers
h = 800 # Hiring cost [$ / worker]
f = 1400 # Firing cost [$ / worker]
c = (250, 500) # Inventory costs [$ / month]
iInit = (8, 3) # Initial inventory
pCost = (6250, 9750) # Production costs [$ / unit]
pWf = (380, 530) # Production workforce requirements [man*hours / unit]
p = 180 # Default productivity of a worker [hours / month]
r = 420 # Regular time employee cost [$ / month]
o = (420/180)*1.5*40 # Overtime employee cost (regular hourly wage * 1.5 * hours) [$ / month]
oLim = 40 # Overtime working limit [hours / month]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Definition of the decision variables
X = { (i, t): LpVariable( name="X-{model}-{month}".format( model = M[i], # Amount of produced models per month
month = t if t>=10
else "0{}".format(t)), # Standardizing the time indices with two digits
lowBound=0 )
for i in range(len(M)) for t in T }
I = { (i, t): LpVariable( name="I-{model}-{month}".format( model = M[i], # Inventory at the end of the month t
month = t if t>=10
else "0{}".format(t)),
lowBound=0 )
for i in range(len(M)) for t in T_ext }
W = { (t): LpVariable( name="W-{}" .format( t if t>=10 # # of workers for t = 0...12
else "0{}".format(t)),
lowBound=0 )
for t in T_ext }
H = { (t): LpVariable( name="H-{}" .format( t if t>=10 # Hired workers for t = 1...12
else "0{}".format(t)),
lowBound=0 )
for t in T }
F = { (t): LpVariable( name="F-{}" .format( t if t>=10 # Fired workers for t = 1...12
else "0{}".format(t)),
lowBound=0 )
for t in T }
O = { (t): LpVariable( name="O-{}" .format( t if t>=10 # Overtime amount for t = 1...12
else "0{}".format(t)),
lowBound=0 )
for t in T }
1
2
3
4
5
6
7
8
9
10
11
12
# Statement of the objective function: The total annual costs must be minimized.
model += lpSum(
[ pCost[i]*X[(i,t)] + # Production costs,
c[i]*I[(i,t)] # and inventory holding costs
for t in T # are summed over each month,
for i in range(len(M) ) ] + # and each product group.
[ r*W[t] + o*O[t] + # Wages,
h*H[t] + f*F[t] # and hiring/firing costs
for t in T ] # are summed over each month.
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# Definition of the constraints
model += (W[0] == wInit # Setting the initial workforce
)
for i in range(len(M)): # Setting the initial inventory levels
model += (I[(i, 0)] == iInit[i]
)
for i in range(len(M)): # Inventory balance / demand satisfaction
for t in T:
model += ( I[(i,t-1)] + X[(i,t)] == I[(i,t)] + D[t-1][i]
)
for t in T: # Workforce balance
model += ( W[t] == W[t-1] + H[t] - F[t]
)
for t in T: # # of overtime workers cannot exceed the total workforce
model += ( O[t] <= W[t]
)
for t in T: # Capacity constraint
model += ( lpSum(X[(i,t)]*pWf[i] for i in range(len(M))) <= p*W[t] + oLim*O[t]
)
1
2
model.solve()
LpStatus[model.status]
1
'Optimal'
1
print("z* = ", value(model.objective))
1
z* = 3143976.3829999994
1
2
3
4
5
6
7
production = []
inventory = []
for i in range(len(M)):
production. append([v.varValue for v in model.variables() if ("X" in v.name) & (M[i] in v.name)])
inventory. append([v.varValue for v in model.variables() if ("I" in v.name) & (M[i] in v.name)])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
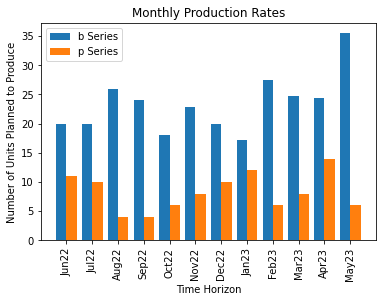
# Plotting the monthly production plan
months = ['Jun22', 'Jul22', 'Aug22', 'Sep22', 'Oct22', 'Nov22',
'Dec22', 'Jan23', 'Feb23', 'Mar23', 'Apr23', 'May23']
X_axis = np.arange(len(T))
for i in range(len(production)):
plt.bar(X_axis - 0.2 + i*0.4, production[i], 0.4, label = "{} Series".format(M[i]))
plt.xticks(X_axis, months, rotation = 90)
plt.xlabel( "Time Horizon")
plt.ylabel( "Number of Units Planned to Produce")
plt.title( "Monthly Production Rates")
plt.legend()
plt.show()
Figure 1. Optimal Monthly Production Plan for the Base Model
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
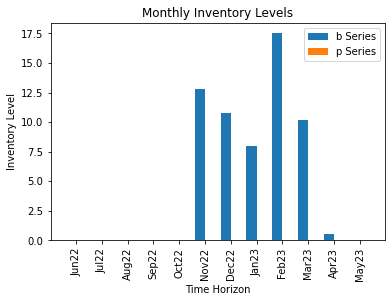
# Plotting the monthly inventory levels
X_axis = np.arange(len(T))
for i in range(len(inventory)):
plt.bar(X_axis - 0.2 + i*0.4, inventory[i][1:], 0.4, label = "{} Series".format(M[i]))
plt.xticks(X_axis, months, rotation = 90)
plt.xlabel( "Time Horizon")
plt.ylabel( "Inventory Level")
plt.title( "Monthly Inventory Levels")
plt.legend()
plt.show()
Figure 2. Optimal Inventory Levels for the Base Model
Extension 1
During the months of December and January you have the option increasing your regular man-hour capacity by bringing temporary skilled workers from another plant. Therefore, there is no hiring cost. Including the relocation cost, the total cost of extra labour force will be $15/hour.
Solution (Extension 1)
1
2
from pulp import *
1
2
3
4
5
# Problem
model = LpProblem( name = "aggregate-planning",
sense = LpMinimize )
1
2
3
4
5
6
# Sets
T = range(1,13)
T_ext = range(13)
M = ("b", "p")
1
2
3
4
# New set: index of the months during which extra workforce can be brought
EM = [7, 8] # December and January
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Parameters
D = ( (28, 14),
(20, 10),
(26, 4),
(24, 4),
(18, 6),
(10, 8),
(22, 10),
(20, 12),
(18, 6),
(32, 8),
(34, 14),
(36, 6) )
wInit = 86
h = 800
f = 1400
c = (250, 500)
iInit = (8, 3)
pCost = (6250, 9750)
pWf = (380, 530)
p = 180
r = 420
o = (420/180)*1.5*40
oLim = 40
1
2
3
4
# New parameter: cost of bringing temporary workers
e = 15 # [$ / hours]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
# Decision variables
X = { (i, t): LpVariable( name="X-{model}-{month}".format( model = M[i],
month = t if t>=10
else "0{}".format(t)),
lowBound=0 )
for i in range(len(M)) for t in T }
I = { (i, t): LpVariable( name="I-{model}-{month}".format( model = M[i],
month = t if t>=10
else "0{}".format(t)),
lowBound=0 )
for i in range(len(M)) for t in T_ext }
W = { (t): LpVariable( name="W-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T_ext }
H = { (t): LpVariable( name="H-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
F = { (t): LpVariable( name="F-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
O = { (t): LpVariable( name="O-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
1
2
3
4
5
6
7
# New decision variable: # of extra working hours supplied by temporary workers
E = { (t): LpVariable( name="E-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in EM }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# Modified objective function
model += lpSum(
[ pCost[i]*X[(i,t)] +
c[i]*I[(i,t)]
for t in T
for i in range(len(M) ) ] +
[ r*W[t] + o*O[t] +
h*H[t] + f*F[t]
for t in T ] +
[ e*E[t]
for t in EM ] # Extra workforce costs
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# Constraints
model += (W[0] == wInit
)
for i in range(len(M)):
model += (I[(i, 0)] == iInit[i]
)
for i in range(len(M)):
for t in T:
model += ( I[(i,t-1)] + X[(i,t)] == I[(i,t)] + D[t-1][i]
)
for t in T:
model += ( W[t] == W[t-1] + H[t] - F[t]
)
for t in T:
model += ( O[t] <= W[t]
)
1
2
3
4
5
6
7
8
9
10
# Modified capacity constraint
for t in T:
if t in EM:
model += ( lpSum(X[(i,t)]*pWf[i] for i in range(len(M))) <= p*W[t] + oLim*O[t] + E[t]
)
else:
model += ( lpSum(X[(i,t)]*pWf[i] for i in range(len(M))) <= p*W[t] + oLim*O[t]
)
1
2
model.solve()
LpStatus[model.status]
1
'Optimal'
1
print("z* = ", value(model.objective))
1
z* = 3143976.3829999994
Extension 2
The gross space requirements of a basic model needs 40 sq meters for storage, whereas a pro model needs 60 sq meters in the finished goods park of the company. The company has total parking area of 500 sq meters. Considering this space constraint would you revise your aggregate plan? The company also has the option of renting extra parking space for a fee of $1 per sq meter per month. Would you consider making a rental agreement, and if so for which months?
Production Engineering and Work Study Department warns you that the standard hours are measured with an error of 10% (i.e., all labor requirement values can change by 10%). Assuming that the storage constraint is active, how sensitive is your optimal plan for scenario to changes in the estimation of labor requirements? Interpret your findings.
Solution (Extension 2)
1
2
3
4
5
# Import libraries
from pulp import *
import pandas as pd # Will be used to generate and export tables
1
2
3
4
5
# Problem
model = LpProblem( name = "aggregate-planning",
sense = LpMinimize )
1
2
3
4
5
6
# Sets
T = range(1,13)
T_ext = range(13)
M = ("b", "p")
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Parameters
D = ( (28, 14),
(20, 10),
(26, 4),
(24, 4),
(18, 6),
(10, 8),
(22, 10),
(20, 12),
(18, 6),
(32, 8),
(34, 14),
(36, 6) )
wInit = 86
h = 800
f = 1400
c = (250, 500)
iInit = (8, 3)
pCost = (6250, 9750)
pWf = (380, 530)
p = 180
r = 420
o = (420/180)*1.5*40
oLim = 40
1
2
3
4
5
# New parameters
e = 1 # Cost of renting extra parking space [$ per sq meter]
gp = 500 # Total capacity of company's goods park [sq meters]
sr = (40, 60) # Space requirements [sq meters]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
# Decision variables
X = { (i, t): LpVariable( name="X-{model}-{month}".format( model = M[i],
month = t if t>=10
else "0{}".format(t)),
lowBound=0 )
for i in range(len(M)) for t in T }
I = { (i, t): LpVariable( name="I-{model}-{month}".format( model = M[i],
month = t if t>=10
else "0{}".format(t)),
lowBound=0 )
for i in range(len(M)) for t in T_ext }
W = { (t): LpVariable( name="W-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T_ext }
H = { (t): LpVariable( name="H-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
F = { (t): LpVariable( name="F-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
O = { (t): LpVariable( name="O-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
1
2
3
4
5
6
# New decision variable: amount of extra space rented
E = { (t): LpVariable( name="E-{}" .format( t if t>=10
else "0{}".format(t)),
lowBound=0 )
for t in T }
1
2
3
4
5
6
7
8
9
10
11
12
# Modified objective function
model += lpSum(
[ pCost[i]*X[(i,t)] +
c[i]*I[(i,t)]
for t in T
for i in range(len(M) ) ] +
[ r*W[t] + o*O[t] +
h*H[t] + f*F[t] +
e*E[t]
for t in T ]
)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
# Constraints
model += (W[0] == wInit
)
for i in range(len(M)):
model += (I[(i, 0)] == iInit[i]
)
for i in range(len(M)):
for t in T:
model += ( I[(i,t-1)] + X[(i,t)] == I[(i,t)] + D[t-1][i]
)
for t in T:
model += ( W[t] == W[t-1] + H[t] - F[t]
)
for t in T:
model += ( O[t] <= W[t]
)
for t in T:
model += ( lpSum(X[(i,t)]*pWf[i] for i in range(len(M))) <= p*W[t] + oLim*O[t]
)
1
2
3
4
5
# New constraint: Goods park capacity
for t in T:
model += ( lpSum(X[(i,t)]*sr[i] for i in range(len(M))) <= gp + E[t]
)
1
2
model.solve()
LpStatus[model.status]
1
'Optimal'
1
print("z* = ", value(model.objective))
1
z* = 3155116.3799999994
1
2
3
4
o = [{'name':name, 'shadow price':c.pi, 'slack': c.slack}
for name, c in model.constraints.items()]
print(pd.DataFrame(o))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
name shadow price slack
0 _C1 None None
1 _C2 None None
2 _C3 None None
3 _C4 None None
4 _C5 None None
.. ... ... ...
70 _C71 None None
71 _C72 None None
72 _C73 None None
73 _C74 None None
74 _C75 None None
[75 rows x 3 columns]
IE 313 - Supply Chain Management
Boğaziçi University - Industrial Engineering Department
GitHub Repository